Bilangan Desimal adalah bilangan yang terdiri dari sepuluh angka tunggal yaitu 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 . Sedangkan bilangan biner adalah Sitem Basis bilangan yang hanya menggunakan dua angka saja yaitu 1 dan 0.
Contoh Latihan Soal Desimal Ke Biner dan Jawabannya
Rumus :
Bagi bilangan desimal dibagi dengan angka 2 jika angka hasil bagi sisa’ bisanya pada angka ganjil, maka tulis 1 dan jika habis dibagi 2 atau dalam arti angka genap maka tulis 0, pembagian dilakukan hingga bilangan desimal < 2 . hasil dari sisa tersebut ditulis dari yang paling bawah ke atas maka akan menghasilkan susunan bilangan biner.
A. Ubah bilangan Desimal(10) berikut ini menjadi bilangan biner (2)
1). 6(10) = ….. (2)
Jawab :
6:2 = Sisa 0
3:2 = Sisa 1
Sisa 1
Maka bilangan biner dari 6(10) adalah 110(2)
2). 72(10) = ….. (2)
Jawab :
72:2 = Sisa 0
36:2 = Sisa 0
18:2 = Sisa 0
9:2 = Sisa 1
4:2 = Sisa 0
2:2 = Sisa 0
1
Maka bilangan biner dari 72(10) adalah 1001000(2)
3). 22(10) = ….. (2)
Jawab :
22:2 = Sisa 0
11:2 = Sisa 1
5:2 = Sisa 1
2:2 = Sisa 0
1
Maka bilangan biner dari 22(10) adalah 10110(2)
4). 81(10) = ….. (2)
Jawab :
81:2 = Sisa 1
40:2 = Sisa 0
20:2 = Sisa 0
10:2 = Sisa 0
5:2 = Sisa 1
2:2 = Sisa 0
1
Maka bilangan biner dari 81(10) adalah 1010001(2)
5). 19(10) = ….. (2)
Jawab :
19:2 = Sisa 1
9:2 = Sisa 1
4:2 = Sisa 0
2:2 = Sisa 0
1
Maka bilangan biner dari 19(10) adalah 10011(2)
Contoh Latihan Soal Biner ke Desimal dan Jawabannya
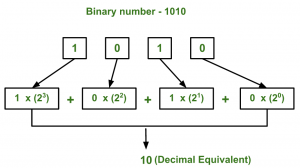
Rumus :
Perhatikan angka biner dari Kanan ke Kiri, masing masing angka biner dari sebelah paling kanan kali dengan 2⁰, dilanjutkan sebelah kirinya dengan 2¹, sebelah kirinya lagi dan seterusnya dengan pangkat yang semakin ke kiri semakin bertambah 2², 2³, 2⁴, 2⁵, 2⁶, 2⁷, 2⁸, 2⁹, ….
B. Ubah bilangan biner (2) berikut ini menjadi bilangan Desimal(10)
1). 110(2) = ….. (10)
Jawab :
110(2) = (0 x 2⁰)+(1 x 2¹)+(1 x 2²)
= 0 + 2 + 4
= 6(10)
2). 1001000(2) = ….. (10)
Jawab :
1001000(2) = 0 + 0 + 0 +(1 x 2³)+ 0 + 0 +(1 x 2⁶)
= 8 + 64
= 72(10)
3). 10110(2) = ….. (10)
Jawab :
10110(2) = 0 +(1 x 2¹)+(1 x 2²)+ 0 +(1 x 2⁴)
= 2 + 4 + 16
= 22(10)
4). 1010001(2) = ….. (10)
Jawab :
1010001(2) =(1 x 2⁰)+0+0+0+(1 x 2⁴)+0+(1 x 2⁶)
= 1 + 16 + 64
= 81(10)
5). 10011(2) = ….. (10)
Jawab :
10011(2) =(1 x 2⁰)+(1 x 2¹)+0+0+(1 x 2⁴)
= 1 + 2 + 16
= 19(10)
Nah itulah contoh soal sederhana Konversi Desimal ke Biner dan sebaliknya beserta cara mengubahnya.